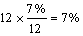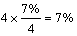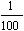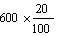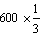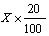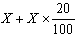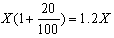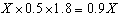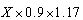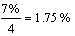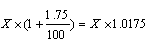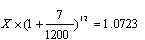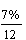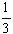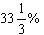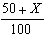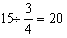מאת: אלעזר ניומן
החלטתי הפעם לכתוב משהו על אחוזים
תוכלו לטעון, בצדק מסוים, מה כבר אפשר לכתוב על נושא שכולם מכירים
ועושים בו שימוש יום-יומי ומי שלא זוכר שיפתח ספר חשבון, יקרא את ההגדרות,
"יתרגל" קצת ובזה תם העניין.
מה שבכל זאת משכנע אותי שכדאי לכתוב משהו על הנושא,
הם כמה מקרים שנתקלתי בהם לאחרונה המצביעים על כך שלמרות שההגדרות
ידועות לכאורה לכל, עדיין יש כמה אי הבנות קטנות (באחוזים)
שמסתובבות בינינו ומתרבות בקצב מעורר דאגה...
להלן כמה דוגמאות.
נסו לאתר את הטעויות בדוגמאות. כולן מהחיים.
1. זיכרון עולה ויורד :
בעל חנות למוצרי מחשב אמר לי שהמחיר של זיכרון שהיה בשימוש לפני שנה
אמנםירד תחילה ב-50% אבל בעקבות רעידת אדמה שהייתה בטיוואן,
הייתהעליית מחירים בשיעור של %80, ולכן המחיר (יחסית לשנה הקודמת)
עלה ב- %30. מה דעתכם ?
2. המתרגמת המתחשבנת :
מתרגמת רצתה להבטיח לעצמה סכום של 2000 ש"חנטו
על עבודת
תרגום שעשתה מחוץ למסגרת עבודתה השוטפת.
מכיוון שעל כל עבודה כזאת היה עליה לשלם מס הכנסה בשיעור של %30,
היא ביקשה עבור העבודה 30% יותר מ 2000, כלומר 2600.
האם אמנם קיבלה את השכר נטו שרצתה ?
3. ההנחה והמע"מ :
לקוח שהובטחה לו הנחה של 10% על כל תיקון במוסך מסוים,
ביקש שההנחה תינתן על המחיראחרי מע"מ, כדי שההנחה תהיה גדולה יותר.
בעל המוסך אמר שהוא ישמח למלא את בקשת הלקוח, אך לדעתו מכיוון שהמע"מ
גדול יותר (%17), משתלם ללקוח לחשב את ההנחה על המחירלפני מע"מ,
כדי שהמע"מ יחושב על סכום יותר קטן. מי צודק ?
4. חיסכון בבנק או חיסכון לבנק:
כאשר התעניינתי בתכנית חיסכון לשנתיים
(הפקדה חד פעמית,ריבית שנתית של %7)
ושאלתי את הפקידה בבנק, האם חישוב הריבית הוא שנתי
( כלומר הריבית מתווספת לקרן רק בסוף השנה ),
רבעוני (הריבית מתווספת לקרן בכל 3 חודשים)
או חודשי (הריבית מתווספת לקרן בסוף כל חודש),
היא אמרה שהחישוב הוא שנתי.
כאשר ציינתי בפניה שיש אי הגינות מסוימת בכך
שכאשר הבנק
הוא המלווה (כמו בהלוואה בנקאית או באוברדרפט )
החישוב הוא בד"כחודשי, ואילו כאשר הלקוח
הוא המלווה
(כמו בתכנית חיסכון ) החישוב הואשנתי,
אמרה הפקידה שזה "בעצם לא משנה" שכן :
בחישוב שנתי הריבית השנתית היא %7,
התשובה המנומקת הנ"ל השאירה אותי ללא מילים...ובחישוב חודשי
>
TD>
>
TR>
>
TABLE>
:
>
TD>
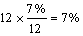
|
|
בחישוב רבעוני הריבית השנתית היא
>
TD>
>
TR>
>
TABLE>
>
TD>
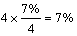
|
|
אפילו שכחתי לשאול מדוע כאשר מדובר בכספי הבנק,
הבנק מעדיף בכל זאת את החישוב החודשי... ?
5. המשכורת שלא עלתה :
לאחרונה סיפרה לי מורה (לא למתמטיקה תודה לאל),
שמשכורתה נטו בחודש האחרון הייתה זהה למשכורתה
נטו בחודש הקודם, למרות שבברוטו הייתה עלייה משמעותית.
ההסבר שלה לתופעה זאת היה, שבעקבות הגידול בברוטו,
המס השולי גם כן עלה וכך התוספת במשכורת התקזזה עם תוספת המס
ו"יצא לי אותו דבר ;".
הזהרתי אותה שלא תעבוד יותר מדי שעות נוספות
שכן עפ"י ההגיון הנ"ל המשכורת נטו שלה עוד עלולה להתחיל לרדת !
אני חושש שהיא לקחה אותי ברצינות...
6. לזרוק את הגבינה או לזרוק את העיתון ?
אודטה אדנין בוודאי גרמה לכמה אנשים בדיאטה,
ליפול
½%
מהכיסא במטבח (יחד עם הגבינה ;189#&))
כשגילתה במדורה (ידיעות 98.12.18
)
את ה"אמת" הכואבת על גבינות דיאטטיות :
"גבינות הכי דיאטטיות זה בלוף מבחינה דיאטטית;".
אני מתאר לעצמי שגם אתם קצת המומים מהמשפט החזק
הזה, אז נוחו כמה דקות ואז המשיכו לקרוא את ההסבר
המתמטי המפורט שמביאה אודטה בהמשך הכתבה :
קחו גבינה %5. ב 100 גרם גבינה כזאת יש 80 קלוריות.
מתוך ה 100 גרם, 5 הגרם של השומן תורמים
5x9=45 קלוריות (גרם שומן9 = קלוריות ) שהן %53 מכלל ה 80 קלוריות
שבגבינה.
"חמישה אחוזים ???;" זועקת-מאשימה אודטה.
"תלוי מאיזה צד בודקיםאת המאזן. מצד היצרנים או מהצד של התוחעס המתעצם...!;"
אודטה רואה, אם כן, את ה 5% המצוינים על האריזה כ "בלוף;",
ומצפה מהיצרנים לומר לנו את האמת :
גבינת ;5 "% שומן" היא בעצם גבינת 53% שומן !!!
לפני שאתם מתחילים לזרוק את הגבינות דלות השומן שלכם מהחלון,
(או על ראשיהם של מנהלי הייצור של תנובהשטראוסטרה)
אנא חשבו רגע על הבעיה הבאה :
קחו בקבוק של 1 ליטר מים מינרלים ( 0 קלוריות) וטפטפו לתוכו
גרם של שמן זית (בשמן זית יש כ 90% שומן,כ 10% מים-וזהו !).
נערו היטב וסגרו את הבקבוק.
נראה סביר לומר שהמוצר המתקבל הוא די דיאטטי (וגם די בריא)- לא ?
אבל...
מהו אחוז השומן של המוצר, לשיטתה של אודטה ?
בטרם אתייחס לבעיות הנ"ל הרשו לי לעשות חזרה קטנה על ה"חומר;".
&אחוז;"
quot;
>
TD>
>
TR>
>
TABLE>
, עפ"י ההגדרה בספרים אינו אלא שם אחר לשבר מאית )
>
TD>
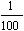
| (
>
TD>
. |
|
זה אמנם נכון, אבל מאז ומתמיד היה הבדל בין האחוזים לשברים רגילים.
בעוד ששברים או מספרים רגילים משמשים גם למדידת כמויות
ספרים
3 )
, ;189#& ליטר חלב, 2500 ש"ח חובה וכדומה ) וגם כאופרטורים
)פעולות על מספרים עם כמויות, >פי 3
SPAN>
כמו למשל ,<190; וכדומה(,
האחוז שימש תמיד (או כמעט תמיד ) כאופרטור בלבד.
לא אומרים ;30 "% מטר" או ;700"% ימים בשבוע ;".
אבל כן אומרים : %20
מהמשכורת, %700של מחיר מוצר
המחיר עלה ב ) %20מהמחיר המקורי) וכו'
כאשר מדובר באופרטור כמו : <20
...אין בד"כ בעיות מיוחדות.
כך ;20 "% של quot;600& הם : 600 x %20 או
>
TD>
>
TR>
>
TABLE>
>
TD>
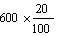
|
|
בדיוק כמו ש;1/3 " של quot;600& הוא :
>
TD>
>
TR>
>
TABLE>
>
TD>
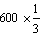
|
|
אבל מה לגבי אופרטור כמו : גדול ב 20% מ...
?
אנשים רבים (ביניהם סוכן ביטוח ותיק שפגשתי) מסתכלים על אופרטור כזה
כעל אופרטורדו-שלבי, שכן לדבריהם, כדי לחשב גידול של X ב 20% יש לעשות
שתי פעולות :
ב. חבר את התוצאה שקיבלת ל X.א
>
TD>
>
TR>
>
TABLE>
. חשב 20% מ X. )
>
TD>
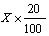
|
)
>
TD>
|
|
כשמדובר באופרטור: קטן ב 20% מ..., החישוב זהה
אלא שהפעם, בשלב ב' ישלחסר את התוצאה מ X במקום לחבר.
כל זה נכון ונחמד, אבל קצת ארוך ומייגע כאשר אופרטורים
כאלו מופיעים בזה אחר זה.
כך, למשל,אם תשתמשו בשיטה זאת כדי לגלות מה קורה לסכום X
כאשר הוא גדל תחילה ב %20, אח"כ קטן ב 30% ולבסוף גדל ב %50,
תצטרכו לעשות 6 פעולות חשבון.
(כאשר כל פעולה מתבצעת על תוצאת הפעולה הקודמת )
או בעיה נפוצה יותר של חישוב הערך הסופי של סכום X אחרי 12 חודשים
של חיסכון ב"ריבית דריבית" חודשית של נניח %5.0.
כאן יידרשו 24 פעולות חשבון !
השאלה המתבקשת, היא, אם כן, האם יש דרך לפשט את החישוב
ע"י הצגת האופרטורים הנ"ל כאופרטוריםחד- שלביים?
התשובה היא חיובית כמובן, והפתרון הוא כה פשוט, שהוא הופך
את כל ההסתכלות על אחוזים כעל "נושא" שיש ללמוד אותו בנפרד
למיותרת.
את זוג הפעולותא. 20% של Xב. חיבור התוצאה של א' ל X,
ניתן להציג ב"מכה אחת" בצורה
>
TD>
>
TR>
>
TABLE>
:
>
TD>
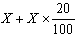
|
|
"כינוס איברים" ( או "הוצאת גורם משותף; ")
של ביטוי זה נותן את הביטוי
>
TD>
>
TR>
>
TABLE>
:
>
TD>
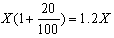
|
|
כלומר האופרטור גדול ב 20% מ...הוא בעצם האופרטור : כפל ב 2
.1.
ע"י החלפת ה ;quot; +"& בסוגריים, ב ;"- " נקבל בדומה, שהאופרטור
קטן ב %20הוא בעצם האופרטור : כפל ב
<8
עד כאן ה"תיאוריה;".
נראה כעת כיצד רוב הבעיות שהצגתי לעיל נפתרות בקלות ע"י עקרון זה :
1. בעיית הזיכרון העולה ויורד :
אם נסמן את המחיר המקורי ב X,אז אחרי ירידת מחירים של %50
ואח"כ עלייה של 80% המחיר יהיה :
>
TR>
>
TABLE>
>
TD>
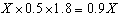
|
|
כלומר לא רק שהמחיר לא עלה ב %30, הואירד ב %10.
2. בעיית המתרגמת המתחשבנת:
הסכום שקיבלה המתרגמת לאחר הורדת מס של 30% היה :
7 = 1820.2600 x 0
כלומר 180 שקל פחות ממה שרצתה.
הסכום שהייתה צריכה לבקש הוא פתרון המשוואה :
>
TR>
>
TABLE>
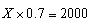
שהוא : X=2857
>
TD>
|
|
3. בעיית ההנחה והמע"מ :
מבחינתו של הלקוח אין הבדל אם ההנחה מחושבת לאחר המע"מ או לפני.
נניח שמחיר התיקון ללא מע"מ הוא X ש"ח אז :
אם קודם מוסיפים את המע"מ ואח"כ מחשבים את ההנחה, המחיר הסופי יהיה :
ואם הופכים את הסדר המחיר יהיה
>
TD>
>
TR>
>
TABLE>
:
>
TD>
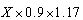
|
>
TD>
. כלומר אותו מחיר סופי |
|
4. בעיית החיסכון :
ראשית,
יש לציין שגם בריבית על הלוואה של הבנק
וגם בריבית של תוכניות חיסכון מדובר במה שקוראים בספרים :
"ריבית דריבית ;",
כלומר בכל פרק זמן קבוע הריבית שהצטברה מתווספת לקרן.
( יוצאים מכלל זה הם תשלומי המשכנתא שבהם הריבית מחושבת
רק על יתרת הקרן. בנושא זה, נדון בהזדמנות אחרת)
האם יש חשיבות לתדירות חישוב הריבית (כלומר
לאורך של אותו פרק זמן קבוע) ?
הבה נשווה בין שלוש האפשרויות שציינו : חישוב שנתי, חישוב רבעוני, חישוב חודשי.
נניח שהפקדנו X ש"ח ב 1 בינואר 2000 בריבית שנתית של %7.
מה יהיה ערך ה X ש"ח ב 1 בינואר ?2001
בחישוב שנתי :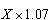
לאחר 3 חודשים ראשונים,
>
TR>
>
TABLE>
הריבית מתווספת לקרןבחישוב רבעוני: הריבית הרבעונית היא
>
TD>
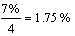
|
|
וערך הכסף הוא עתה
>
TD>
>
TR>
>
TABLE>
:
>
TD>
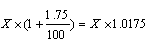
|
|
לאחר עוד 3 חודשים הסכום האחרון גם כן צובר ריבית ולכן נקבל :
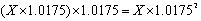
וכך הלאה...
בסוף השנה ערך ה X שקלים יהיה :
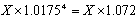
כלומר הריבית השנתית ה"אפקטיבית" עלתה מ 7% ל %2.! 7
בחישוב חודשי :
שבסוף השנה ערך X השקלים יהיה
>
TD>
>
TR>
>
TABLE>
:
>
TD>
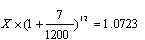
|
|
הריבית החודשית היא :
>
TD>
>
TR>
>
TABLE>
>
TD>
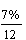
|
>
TD>
. בדומה לחישוב שעשינו לעיל נקבל |
|
כלומר ריבית שנתית "אפקטיבית" של %23.7.
שוב עלייה קטנה.
אפשר לטעון שההבדלים אינם משמעותיים או כמו שאומרים " זה כסף קטן;".
נכון. אבל למי שלא יודע- את הכסף הגדול עושים הבנקים
מה"כספים הקטנים " שלנו...
5. בעיית המשכורת הלא עולה :
ראשית אבהיר שאינני בא להצדיק כאן את שיעורי מס ההכנסה
הגבוהים שאנו משלמים ואני בהחלט מצטרף לדעתם של אלו
הסבורים שיש להוריד את שיעורי המס.
יחד עם זאת צריך להבהיר שלא משנה כמה שיעורי
המס יעלו (כל עוד שיעורי המס קטנים מ %100)
כל עלייה בשכר הברוטו, גוררת בהכרח עלייה כלשהי
בשכר נטו.
כדי להבהיר זאת, נניח שהמורה משתכרת 3800 ש"ח.
מס הכנסה מחלק סכום זה לשני סכומים ( החלוקה כאן היא עפ"י
מדרגות המס מינואר 2000, אך אין חשיבות לשיעורי המס
עצמם- העיקר הרעיון )
3800 = 1940 + 1860
על הסכום ה"ראשון;"-1940 ישולם מס בשיעור %10
ואילו על הסכום ה"שני;"- 1860, ישולם מס של %20.
נניח כעת שהתווסף למשכורת עוד 120 שקל.
שיעורי המס על שני הסכומים הראשונים אינם משתנים.
ה 120 ש"ח הנוספים יחולקו שוב לשני סכומים: 120 = 90 + 30.
על ה-90 ש"ח ה"ראשונים" (שנמצאים עדיין במדרגת המס האחרונה)
ישולם מס של %20.
על ה 30 ש"ח הבאים ישולם כבר מס של %30.
גם אם נמשיך לצרף סכומים נוספים למשכורת
לא יהיה שום שינוי בשיעורי המס של הסכומים ה"ראשונים;".
שיעורי המס הגדולים יותר יחולו רק על הסכומים "האחרונים;".
מכיווןשכל שיעורי המס קטנים מ 100% ( שיעור המס הגבוה
ביותר הוא %50), מכל עלייה (תוספת) של משכורת
תמיד נשאר סכום חיובי כלשהו.
כלומר, כל עלייה בברוטו גוררת בהכרח עלייה כלשהי בנטו.
אם בכל אופן נראה לכם שמשכורתכם ברוטו עלתה
והנטו נשאר (או ירד), אז, או שיש טעות (כן, גם זה קורה לפעמים )
או שמדובר במצבים מיוחדים
( כמו למשל זיכויים חד פעמיים, הטבות ממקום העבודה המופיעות
כהכנסה נוספת בברוטו ולא בנטו וכדומה ).
בכל מקרה כדאי לבדוק.
6. בעיית הגבינות :
הדוגמא של השמן זית בתוך הבקבוק מים מינרלים נועדה
להראות את האבסורד שבטענה של אודטה.
מכיוון שבשמן זיתכל הקלוריות מקורן בשומן, הרי ש %100
מכל הקלוריות הם שומן ולכן לשיטתה של אודטה,
זהו מוצר של 100% שומן!
ולגופו של עניין- מה שחשוב מבחינה דיאטטית ובריאותית
הוא איזה חלקמהמזון שאנו אוכלים הוא שומן, ולא איזה
חלקמהקלוריות שאנו אוכלים הוא שומן.
מי שאוכל 100 גרם גבינת 30% שומן, אוכל 30 גרם שומן
ואילו מי שאוכל אותה כמות של גבינת 5% שומן,
אוכל 5 גרם שומן בלבד, כלומר כמות קטנה פי 6,
ואין כאן שום "בלוף;".
מי שמתעניין רק בכמותהקלוריות שהוא אוכל,
יכול בכלל להתעלם מאחוז השומן ולהסתכל ישירות על
כמות הקלוריות ל 100 גרם המופיע היום על רוב מוצרי המזון.
ולסיום מספר בעיות וחידות בנושא אחוזים ( תשובות בנספח )
1. שלושה מומחים לחיסכון באנרגיה הגיעו למפעל מסוים כדי
לצמצם את צריכת החשמל בתהליכי הייצור.
לראשון הייתה הצעה שמביאה לחיסכון מיידי של 50% מהצריכה,
לשני הייתה הצעה שמביאה לחיסכון של 20% מהצריכה
ולשלישי הייתה הצעה שמביאה לחיסכון של 30% בצריכה.
ההשפעות של כל אחת מההצעות הן בלתי תלויות זו בזו.
כתוצאה מקבלת כל שלוש ההצעות, החיסכון בצריכה היה %100
כלומר המפעל כבר לא צרך חשמל בכלל !
הגיוני ?
לא כל כך.
אז מה באמת היה החיסכון בצריכה ?
2. בשנה מסוימת מדד המחירים לצרכן ירד ב %25. ( מה יש, אסור לפנטז? )
בכמה אחוזים עלה השכר הריאלי כתוצאה מכך?
3. במדינה ששר האוצר מפנטז עליה בלילות, משלמים מספר אחוזי מס הכנסה
כמספר הדולרים שמרוויחים. (לדוגמא מי שמרוויח 1 דולר משלם
1% מס, מי שמרוויח 2 דולר משלם 2% מס, מי שמרוויח 100 דולר משלם
אתכלמשכורתו למס ומי שמרוויח יותר מזה משלם את כל משכורתו ועוד
חייב כסף למדינה... ).
מהי המשכורת האופטימלית במדינה זו- מנקודת מבטו של האזרח כמובן ?
4. חידה רוסית עתיקה מספרת על אב ובנו שקטפו המון פטריות ביער.
בפטריות הטריות שקטפו היו 90% מים ולכן הם הניחו אותן לייבוש בשמש.
לאחר זמן, אחוז המים ירד ל 60% וכתוצאה מכך משקל הפטריות
ירד ב 15 ק"ג. כמה ק"ג פטריות קטפו בתחילה ?
5. 45% מכלי השחמט על הלוח הם שחורים. כמה כלים לבנים על הלוח ?
אם לא הצלחתם לפתור חלק מהשאלות אל תתייאשו.
זיכרו את דבריו של אותו מורה, שאמר להוריו המיואשים של ילד שהישגיו היו נמוכים ביותר :
" התעודדו ! בנכם נמצא בין 99% התלמידים הטובים ביותר בכיתה ;!!! "
להשתמע
אלעזר ניומן
תגובות,שאלות,הצעות,רעיונות,net
בדיחות נא לשלוח ל:.online-barak@beezle
נספח : תשובות לבעיות וחידות
1. אם צריכת החשמל בתחילה הייתה X. אז אחרי שיושמו כל ההצעות,
הצריכה הייתה :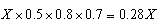
כלומר חיסכון ב 28% מהצריכה.
2. ירידת מחירים ב 25% אומרת שהמחירים הם 75.0 או ;190#& מהמחירים בתחילת השנה.
כלומר עם שקל אחד אפשר לקנות פי 4/3 ממה שאפשר היה לקנות בתחילת השנה.
כלומר השכר הריאלי עלה ב
>
TD>
>
TR>
>
TABLE>
>
TD>
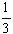
|
או
>
TD>
|
>
TD>
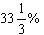
|
|
3.אפשר כמובן לפתור את השאלה בעזרת חשבון דיפרנציאלי אך
במקום זאת אפשר לשים לב שעל משכורת של 50 + X
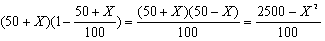 משלמים מס של
>
TD>
>
TR>
>
TABLE>
משלמים מס של
>
TD>
>
TR>
>
TABLE>
>
TD>
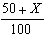
|
>
TD>
. כלומר ההכנסה הנותרת היא |
|
כדי שביטוי זה יהיה מקסימלי, X כמובן צריך להיות שווה ל 0 כלומר
המשכורת האופטימלית היא 50 דולר.
4. אחוזהפטריות נטו עלה מ 10% ל %40. מכאן שהמשקל הכללי של
הפטריות קטן פי 4 ולכן משקלן כעת רבע ממשקלן המקורי.
כלומר 15 ק"ג מהווים 3/4 מהכמות ההתחלתית.
ולכן הכמות ההתחלתית הייתה
>
TD>
>
TR>
>
TABLE>
.
>
TD>
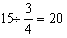
| ק"ג
>
TD>
. |
|
5. אם 45% מהכלים הם שחורים, אז 55% הם לבנים.
כלומר יחס מספרי הכלים 45:55 או 9:11.
מכיוון שיש לכל היותר 16 כלים מכל צבע, בהכרח היו 9
כלים שחורים ו 11 לבנים.
מאמרים נוספים בפינה: חשבון מהחיים