מאת: אלעזר ניומן
מבין המקצועות הנלמדים בביה"ס היסודי והתיכון, הגיאומטריה אינה נמנית עם הפופולריים
שבהם. נכון שהמתמטיקה בכלל נתפסת אצל תלמידים כמקצוע טכני ומנותק מהמציאות,
אך הגיאומטריה היא בעייתית במיוחד במובנים אלו, שכן היא גם "מופשטת" וגם קשה.
(העובדה שדווקא תחום כל כך חזותי, הגיוני ואינטואיטיבי נחשב ל"מופשט;"
מעוררת סימני שאלה על שיטות ההוראה בתחום זה...)
תלמידים לא נוטים להתפעל מהמבנה הלוגי- דדוקטיבי המפואר שיצר אוקלידס,
לא ממש מבינים את הצורך הקטנוני הזה לציין את ה"נתון;"
וה "צ.ל." בכל פעם שעולה איזו "טענה" חדשה,
ובכלל הצורך האובססיבי הזה של מורים למתמטיקה להוכיח כל דבר...
אני מניח שרוב התלמידים היו שמחים להסתפק בהוכחה האחידה הבאה
לכל הטענות והמשפטים הידועים :
1. ;nbsp; & אוקלידס ידע מצויין גיאומטריה.
2. ;nbsp; & אוקלידס אמר שהמשפט נכון.
מ1 ו2 נובע שהמשפט נכון. מ.ש.ל.
הצטרפותם של אנשי חינוך, מדענים ואפילו מתמטיקאים,לביקורת על הגיאומטריה האוקלידית
(מסיבות שונות לחלוטין מאלו של התלמידים-ראה להלן) לא תרמה כמובן למעמדו של המקצוע
וגרמה לאיזו דעה כללית מוטעית שאין תועלת בלימודו.
מפעם לפעם אני שומע מפיהם של "מלומדים" (בעיקר אנשי מדעי הרוח, שמגלים בהרצאותיהם
כשרון גדול למציאת המרחק הארוך ביותר בין שתי נקודות...)
על קריסתה כביכול של הגיאומטריה האוקלידית בהיותה
"בלתי מתאימה למציאות הפיזיקלית לאור תורת היחסות של איינשטיין;"... (ברור לכולם ? )
מבלי להיכנס יותר מדי לפרטים, אומר רק שהביקורת על הגיאומטריה של אוקלידס
היא יותר על מה שאין בה מאשר על מהשיש בה.
(אי טיפול במושג ה"סדר" של נקודות על ישר ומושג ה"פנים" ו ה"חוץ" של צורה,
הפרדה לא מוצדקת בין המישור למרחב, דגש מוגזם על לוגיקה במקום קירובים אלגבריים
ויישומים, וכמובן בעיות לוגיות בהגדרות והוכחות.
רבים מ"ליקויים" אלו תוקנו ע"י המתמטיקאי דיוויד הילברט (1862-1943) שהרחיב
ושיפץ את עבודתו של אוקלידס והמשיך את מורשתו ה"אקסיומטית;").
אשר ל "חוסר ההתאמה למציאות הפיזיקלית;", אזכיר רק שגיאומטריות אוקלידיות ואחרות
אינן מתיימרות לתאר מציאות פיזיקלית כזאת או אחרת,
אלא רק לבנות מערכת של משפטים ואקסיומות בעלת חוקיות פנימית (הגיונית) מסוימת.
השאלה אינה האם גיאומטריה מסוימת נכונה או לא נכונה
אלא האם,במצב מסוים,היאשימושית או לא.
ניתן לומר שנגרים, שרטטים, אדריכלים, מהנדסים, רצפים, בנאים ועוד,
הגם שאינם מסתובבים עם ספר "היסודות" של אוקלידס בכיס העליון של הסרבל,
עושים (במודע או שלא במודע) שימוש יום-יומי במשפטים ובמסקנות של הגיאומטריה האוקלידית.
דוגמא אחת היא הדרך שבה בנאים בודקים ששני קירות ניצבים זה לזה בעזרת "מטר; ":
מסמנים על קיר אחד נקודה הנמצאת במרחק של 3 ס"מ מהפינה,
על הקיר השני מסמנים נקודה באותו הגובה הנמצאת 4 ס"מ מהפינה
ומודדים את המרחק בין שתי הנקודות.
עפ"י משפט פיתגורס הקירות יהיו ניצבים אם ורק אם המרחק הנמדד הוא בדיוק 5 ס"מ
(מצב נדיר למרבה הצער...).
השימוש בגיאומטריה האוקלידית בשרטוט ובגרפיקה הוא מובן מאליו
וניתן לומר שהגיאומטריה בתחומים אלו היא חלק אינטגרלי של המקצוע.
אך לעיתים קורה שהגיאומטריה צצה באופן לגמרי לא צפוי
ומשפט שנראה כתיאורטי לגמרי מתגלה כבעל חשיבות פיזיקלית רבה.
דוגמא כזאת שנעסוק בה בהמשך המאמר היאמשפט החפיפה: "צלע צלע צלע;".
למי שמשפט זה נשמע כמו פרסומת לשמפו חדש (עם שלוש פעולות לחיזוק השיער... )
הנה תזכורת קצרה :
שני משולשים שאורכי צלעותיהם שווים בהתאמה- חופפים(כלומר זהים מבחינה צורנית.)
מסקנה ממשפט זה ( או אם תרצו, ניסוח שקול למשפט ) היא :
שלוש הצלעות של המשולש קובעות את צורתו של המשולש.
כלומר משולש הוא צורהיציבה ( באנגלית: rigid),שכן אורכי צלעותיו קובעים את זוויותיו
ולכן אין לו "חופש" לשנות את צורתו.
כדי להבין טוב יותר את המשפט (וכן כדי לבצע עוד כמה ניסויים שיבואו בהמשך)
רצוי להצטייד בשלב זה ב"ערכת בנייה" הכוללת :
1.;2 חבילות של קשיות לשתייה.
2.;nbsp; & קופסת נעצים (רצוי ארוכים) כדי לחבר יחד שתי קשיות או יותר.
3.;nbsp; & מספריים לחיתוך הקשיות.
את הקשיות רצוי לשטח" (כלומר להפוך לשטוחים) כדי למנוע את בריחתן מהנעצים.
נבנה כעת משולש ומרובע מקשיות באורכים שונים (ראה ציור 1).
הנעצים מחברים שתי קשיות יחד אך אינם מגבילים את תנועת הקשיות.
נקודת חיבור מסוג זה נקראת "פרק;".
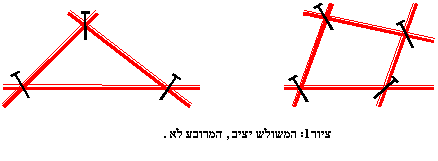
המשולש הוא יציב ולכן לא נצליח לשנות את צורתו.
המרובע לעומת זאת אינו יציב ומשנה את צורתו בקלות רבה.
שאלה טבעית שמתעוררת כאן היא כמה קשיות יש להוסיף למרובע כדי לייצב אותו ?
>
TD>
|
|
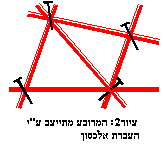
גם ללא ביצוע הבנייה ניתן לראות בקלות שקשית
אחת לאורך אחד מאלכסוני המרובע תספיק
(ראה ציור 2)
שכן ה"מבנה" מורכב כעת ממשולשים
אם נראה לכם כעת שנושא היציבות של צורה (או שלד של גוף במרחב) הוא עניין פשוט, ההופכים אותו ליציב
>
TD>
>
TR>
.
אז זה הזמן לציין שנושא זה העסיק מתמטיקאים ומהנדסים שנים לא מעטות
ומהווה תחום תיאורטי בפני עצמו הקרוי : rigidity theory.
כדי לקבל תחושה על הקשיים שיש בתחום זה, הנה שאלה לדוגמא.
הסתכלו בצורות שבציור 3 ונסו לקבועאיזו צורה יציבה ואיזו לא?
מומלץ כמובן לבדוק את תשובותיכם ע"י בניית הצורות.
זה דורש קצת סבלנות אך מניסיון אוכל לומר שזה שווה את המאמץ.
שימו לב שהנעצים או ה"פרקים" מיוצגים הפעם באמצעות עיגולים שחורים.
כמו כן שימו לב שצורה ג' מורכבת מ-14 חלקים המצוינים בצבעים שונים.
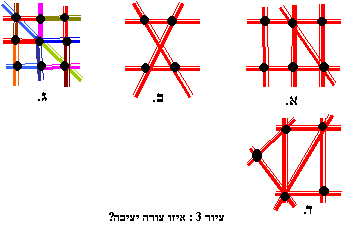
תשובה : צורות א' ב' ג' אינןיציבות
. צורה ד' יציבה.
את חוסר היציבות של צורות א', ב', ג' אשאיר כתרגיל מחשבתי
(לאלו שלא טרחו לבנות את הצורות כמובן ).
שימו לב שכדי להראות חוסר יציבות יש לצייר צורה שכל צלעותיה שוות לצורה המקורית
אך זוויותיה שונות.
העובדה שצורה ד' יציבה היא די ברורה לעין, שכן היא מורכבת ממשולשים המייצבים אותה.
כך גם כמובן, לגבי כל צורה אחרת המורכבת ממשולשים.
כלומרתנאי מספיק ליציבות של צורה, היא שהצורה תהיה מורכבת ממשולשים בלבד.
זה כמובן מעורר את השאלה : האם התנאי שצורה תהיה מורכבת ממשולשים הוא גם
תנאיהכרחי ליציבות ?
במילים אחרות, האם צורה שאינה
מורכבת כולה ממשולשים היא בהכרח לא יציבה ?
אלו שיש להם דגמים מוכנים של הצורות לעיל יוכלו להיווכח מיד שהתשובה
לשאלה האחרונה היא שלילית.
פשוט הוסיפו עוד אלכסון אחד קטן לצורה ג' (ראה ציור 4 ) ותקבלו צורה יציבה למהדרין !
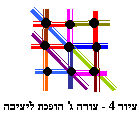
מהו אם כן תנאי הכרחי ליציבות ?
תנאי הכרחי ומספיק ליציבות במבנה העשוי משריג מלבני (כמו צורה ג' הנ"ל)
נוסח והוכח לראשונה ע"י המתמטיקאים Crapo ו Bolker ב 1977.
אדגים את טענת Bolker-Crapo בשריג 2 על 2 כמו צורה ג' לעיל.
שריג כזה מורכב מ2- שורות ו-2 עמודות.
ייצוב השריג תלוי כמובןבמספרם ובמיקומם של האלכסונים הקטנים שבתוך השריג.
נסמן את שתי השורות ב-ש1 (שורה עליונה) ו-ש2 (שורה תחתונה)
ואת שתי העמודות ב-ע1 (עמודה שמאלית) ו-ע2 (עמודה ימנית ).
נשרטט דיאגרמה שמורכבת משתי קבוצות של נקודות.
קבוצה אחת שתייצג את השורות וקבוצה שנייה שתייצג את העמודות (ראה ציור 5a).
כעת נעביר קו בין כל שורה ועמודה שיש להם אלכסון משותף.
כך למשל בציור ג' המקורי יש אלכסון משותף לשורה 1 ולעמודה 1
ולכן נעביר קו בין ש1 ל-ע1.
באותו ציור יש גם אלכסון משותף לשורה 2 ולעמודה 2,
ולכן נעביר קו גם בין ש2 ל- ע1 (ראה ציור 5b)
אם נצייר גרף כזה עבור ציור ג' עם תוספת האלכסון (ציור 4) נקבל את הגרף שבציור 5c.
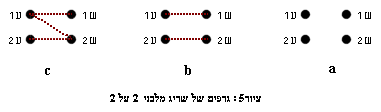
מה ההבדל בין גרף 5b לגרף ? 5c
גרף 5c הוא גרף קשיר
, כלומר קיים מסלול על הגרף המקשר כל נקודה עם כל נקודה אחרת.
גרף 5b, לעומת זאת, אינו קשיר.
הבדל זה הוא המפתח לזיהוי שריגים יציבים ולא יציבים :
טענת Bolker-Crapo : שריג ריבועי הוא יציב אם ורק אם הגרף המתאים לו הוא קשיר.
טענה זאת מאפשרת לנו לוותר על קשיות, נעצים וכו' ולחזור לעט ולנייר.
(לא לחינם מכנים את המתמטיקה "האומנות של העצלנים...;")
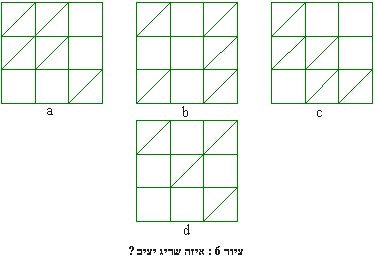
נסו כעת להשתמש בטענת Bolker-Crapo כדי למצוא את השריג היציב
מבין ארבעת השריגים הבאים של 3 על 3 שבציור 6.
(הניחו כמובן, שבכל קדקוד שבשריג יש "פרק" המאפשר חופש תנועה לכל הקטעים היוצאים ממנו).
את הפתרון תמצאו בנספח.
שאלה נוספת שמתעוררת כאן היא מהו המספר המינימלי של אלכסונים הדרושים
כדי לייצב שריג כזה ?
ובאופן כללי מהו מספר האלכסונים המינימלי הדרושים לייצב שריג של ? mxn
כלומר שריג עם m שורות ו-n עמודות.
גם את התשובה לשאלה זו,יחד עם מקורות לקריאה נוספת,תמצאו בנספח.
שאלה בוערת יותר היא מה קורה במרחב ?
כלומר, אם אתם מתכננים לבנות "שלד" במרחב, כיצד תדעו אם הוא יהיה יציב או לא.
כך, למשל,האם השלד של גוף כמו תיבה או קובייה שבו יש חופש בקדקודים
(כלומר אין "הלחמה" בקדקודים ) הוא יציב?
אם הרכבתם פעם "סוכה לנצח" העשויה משלד
>
TD>
|
>
TD>
|
|
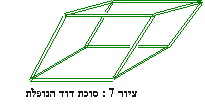
קובייתי של מוטות ברזל עם חיבורים
מולחמים בקדקודים, אז בוודאי שמתם לב
שיציבות זה לא הצד החזק שלה.
(ראה ציור 7)
ראשית, מסתבר שהסוכה היא אולי "לנצח;", אבלההלחמות לא ממש, אלא כמה שנים פחות...
>
TR>
>
TABLE>
שנית, גם אם ההלחמות קיבלו ברכה מיוחדת לאריכות ימים,
הסוכה עדיין מגלה גמישות מפתיעה שהולכת וגדלה, וכשמגיעה "שמחת תורה" יחד
עם רוחות קלות של תחילת הסתיו, היא כבר "רוקדת" בהתלהבות רבה...
מיותר לציין שאם הפינות הן "פרקים;", כלומר אינן מולחמות,
הסוכה שלכם תהיה כבר בהתחלה סוכה דו ממדית !
כלומר שלד של תיבה אינויציב
.
כיצד נוכל לייצב אותה ? ובאופן כללי מה הם התנאים ההכרחיים והמספיקים ליציבות ?
ובכן כאן, כצפוי, העסק קצת מסתבך שכן במרחב,
המתמטיקאים מבחינים בין "לא יציב;non rigid) ") לבין "טיפ טיפה לא יציב;"
(שזה תרגום חופשי שלי למונח ""infinitesimally non rigid.
אשמח לשמוע ממי שמכיר, את התרגום העברי הרשמי למונח זה ! )
לא אכנס כאן להגדרה הפורמלית, רק אציין שמבנה "טיפ טיפה לא יציב" הוא יציב,
פרט לתנועה זעירה מאוד של הקדקודים תחת לחץ.
על אף שהתנועה זעירה ביותר ("אינפיניטסימלית;"), יש הסכמה בין מהנדסי הבניין
שמבנה כזה אינו טוב לבריאות...
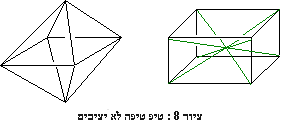
{שתי דוגמאות למבנים "טיפ טיפה לא יציבים" הם שלד של תיבה
שהוסיפו לו ארבעה אלכסונים המחברים קדקודים נגדיים,
וכן שלד של תמניון (octahedron) גוף בעל 8 פיאות שכולן משולשים! (ראה ציור {(8
בעיה שנייה היא שבמרחב אין תנאי פשוט כמו תנאי Bolker-Crapo
המאפשר זיהוי שלדים יציבים, לא יציבים ו"טיפ טיפה לא יציבים;".
מה ידוע בכל זאת ?
ובכן מבלי להכנס לעובי הקורה (מה שידרוש מאמר נוסף) אציין רק שגם כאן כצפוי,
לחלוקה של צורה (או פיאה) למשולשים יש תפקיד מרכזי.
בשנות ה-40,המתמטיקאי הרוסי Alexandrov.D.A,הוכיח שכל שלד של פיאון קמור
(כלומר גוף ללא חורים או "שקעים" שפיאותיו עשויות מצולעים עם 4 צלעות ומעלה )
ניתן לייצוב (מלא) ע"י העברת אלכסונים, כך שכל הפיאות יהיו מחולקות למשולשים.
המשמעות של משפט זה לגבי סוכתנו הנופלת (כלומר שלד של תיבה) היא,
ש-6 מוטות נוספים,מוט אחד אלכסוני בכל פיאה, ייצבו אותה ייצוב מוחלט ונצחי.
(במקרה זה 6 מוטות נוספים הוא גם המספר המינימלי של מוטות נוספים הנדרשים לייצוב)
תחום שבו תכונת היציבות של המשולש מנוצלת היטב היא בהנדסת בנין.
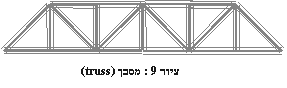
בתחום זה נעשה שימוש רב במבנה בסיסי הנקרא "מסבך;truss) ").
המסבך, שמשמש לבניית גשרים ולתמיכת מבנים,כולל "צלעות" (שהן בד"כ מוטות של פלדה)
המחוברות זו לזו בפרקים, ויוצרות יחד מבנה תומך של משולשים
(ציור 9 מראה סוג אחד של מסבך הנקרא מסבך Warren)
כאשר החיבורים בין הצלעות הם "פרקים" או כמעט "פרקים" (כלומר מאפשרים חופש מסוים)
הן נתונות בעיקר למה שהמהנדסים קוראים מאמצי "לחיצה" ו"מתיחה" ופחות למאמצי "כפיפה;".
עובדה זו מאפשרת למסבך לעמוד בעומס גדול יותר מאשר מבנה הדורש הלחמת החיבורים
שבין הצלעות (כמו מבנה שאינו מורכב ממשולשים), שכן מבנה כזה נתון גם למאמצי כפיפה.
(תודתי נתונה לד"ר מ.מודריק, ד"ר א.זינגר ומר י. לימונד על הבהרת נקודה זאת.)
שיטת בנייה המבוססת כולה על שימוש במסבכים תוך ניצול יכולת עמידתם המוגברת,
היא שיטת ה : staggered truss system.
בשיטת בנייה זאת המסבכים מהווים את השלד התומך בתקרות וברצפות, ומאפשרים
(בזכות כושר עמידתם המוגבר) בניית חללים גדולים ללא עמודי תווך.
(בארה"ב נעשה שימוש רב בשיטה זאת, בעיקר לבניינים רבי קומות.
בארץ- בי"ח איזנברג ביפו וכן מבנה מגורים ביזרעליה שבנווה שאנן בחיפה, נבנו בשיטה זו.
הפעם מגיעה תודה למהנדסת גילה גילאי על האינפורמציה הנוגעת לשיטת בניה זו)
גם שלד העץ התומך בגגות רעפים עשוי ממסבכים פשוטים ("אגדים" בשפה מקצועית),
כאשר החיבורים בין קורות המסבכים נעשה במסמרים המהווים מעין "פרקים;".
כשמדברים על השימוש במשולשים בבניין ובארכיטקטורה,
אי אפשר שלא להזכיר גם את הכיפה הגיאודזית (geodesic dome) של
הארכיטקט האמריקאי Buckminster Fuller שגם בה, המשולש ממלא תפקיד נכבד.
(לFuller ולכיפה הגיאודזית המהווה דוגמא מאלפת של יישום מתמטיקה
וגיאומטריה בארכיטקטורה, אקדיש את אחד המאמרים הבאים.)
ולסיום, ציטוט חשוב.
כשהתייעצתי עם ידידי ב.ס. על כותרת לכתבה זו,הוא חשב לרגע,
הסתכל סביב לוודא שאין איש שומע ואז לחש לאוזני :
" הפתרון : קליניקה און לפוליגון ;".
הכותרת נדחתה משיקולים קואליציוניים אך לא יכולתי שלא להביא את
פנינת הלשון הנ"ל בפני הקוראים.
מה שמזכיר לי עוד הערה חשובה.
אם נתפסתם ן ע"י בןבת זוגכם עם המאהבמאהבת, יש לכם עכשיו תירוץ מצוין :
עשיתם את הכל לחיזוק הקשר הזוגי שכן קראתם במאמר, שמשולש תורם ליציבות...
להית' בשמחות
אלעזר ניומן
נ.ב. תודה מיוחדת לאשתי גב' חווה ניומן על עריכת המאמר.
תגובות
, הערות, הצעות, net
בדיחות ורעיונות לשלוח ל.online-barak@beezle
נספח
הגרפים של הצורות האחרות אינם קשירים ולכן הצורות אינן יציבות
.הגרף שלה הוא מהצורה
>
TD>
>
TR>
>
TABLE>
>
TD>
|
>
TD>

|
>
TD>
| וזהו גרף קשיר
>
TD>
. |
|
הצורה היציבה היחידה בציור 6 היא צורה 6c
.|
|
<
מספר האלכסונים המינימלי הנדרשים לייצוב שריג מלבני של 3x3 הוא 5.
|
>
TD>
>
TR>
1.|
>
TD>
|
>
TD>
ולכן 6c הוא גרף עם ייצוב מינימלי.
באופן כללי, מספר האלכסונים המינימלי הנדרשים לייצוב
של שריג מלבני של mxn הוא 1-m+n.
(עובדה זאת נובעת מכך שהגרף של ייצוב מינימלי הוא "עץ;"
,כלומר גרף ללא
"מעגלים; ").
לקריאה נוספת : |
|
>
TD>
>
TR>
2.|
>
TD>
|
>
TD>
rigidity (by Robert Connelly)
>
UL>
>
DIV>
- 7.Mills chapter 2.M.J Gruber and.M.D "Handbook of convex geometry " by8
.7, 18."Connections :The geometric bridge between art and science " by Jay Kappala sections 4Dewdney Scientific American may 1991
.K.A Mathematical recreations
|

